Newton’s laws are a story of arrows. Not physical arrows (although that’s sometimes the case) but a kind of mathematical arrow known as a vector.
The simple concept of a vector is something that has both a quantity (magnitude) and a direction. For example, if you’re traveling in a car, the velocity of your car is a vector that determines both your speed and the direction in which you are moving. Newtonian physics is largely concerned with forces, which are vectors representing the push or pull on an object in a particular direction. One of the key aspects of Newton’s laws is that forces are exerted between objects. If you push on an object to get it to moving, you can feel the object pushing back against your hand. That makes sense if two objects are physically touching, but what about if they aren’t touching. What about, say, the Earth and the Moon?
The Moon doesn’t drift through space, but rather orbits the Earth. Newton reasoned the Earth must be pulling on the Moon to keep it in orbit. A force of gravity, if you will. Newton’s breakthrough was to recognize that the gravitational force that pulls apples to the Earth is the same gravitational force that holds the Moon in orbit around the Earth, or the planets in orbit around the Sun. Every body in the universe must pull upon every other body with a mutual attraction. This law of universal gravity worked so well Newton was able to derive Kepler’s laws of planetary motion as a consequence of gravity. It connected earthly motion with heavenly motion and laid the foundation for modern astrophysics.
But there was still the issue of how distant objects can feel such a force. How does the Moon “know” the Earth is nearby and “know” to be pulled towards it? For a time you could brush aside the question and focus on solving Newtonian problems, but the question raised its head again in the study of electricity. By the 1700s we understood that electricity came in two forms of charge, positive and negative. Like gravity, charges exerted forces on other charges, even separated by some distance. Sure, the force got weaker with distance, but it was always there.
One proposed answer is that charges must reach out to each other with some kind of energy. That is, a charge is surrounded by a field of electricity, a field that other charges can detect. Charges possess electric fields, and charges interact with the electric fields of other charges. For this to work, the electric field must be a vector field. At each point in space the electric field must have a magnitude and a direction. When a charge detects an electric field, it therefore knows the magnitude and direction of the force acting on it.
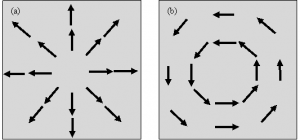
For any vector field you can trace paths through the field known as field lines. If you start at a particular point in the vector field, you can take a small step in the direction the vector is pointing. At your new position take a step in the direction of the vector. Keep doing that, and you trace a line following the vectors of the field. If you trace field lines for an electric field, it turns out that they always draw a path from some positive charge and to some negative charge. This is because positive charges always push other positive charges away, while negative charges always pull positive charges towards them. As a result, electric field lines always spread out of positive charges and collapse into negative ones. In mathematics this property is known as divergence.
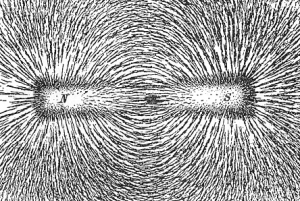
Field lines that have a beginning and an end will always be divergent. But what if you traced a path through space and eventually found yourself back where you started? Instead of a finite line, it would form a loop without end. In mathematics this is known as curl. It turns out that magnetic fields have exactly this property. While charges are always either negative or positive, magnets always come in pairs of poles (north and south). Magnetic field lines spread out from north poles, but they always loop back on themselves, coming together at a south pole. Because of magnetic curl, you can never have just a north pole or just a south pole, and in fact if you break a magnetic in half you will get two magnets.
So the electric field is a vector field with divergence, and the magnetic field is a vector field with curl. But mathematically a general vector field can have a combination of divergence and curl. The mathematics would therefore seem to imply that electric fields and magnetic fields are simply two parts of the same vector field. This is actually true. Electric and magnetic fields are each part of a more general electromagnetic field. Not only that, electric fields that change over time (say from moving charges) can induce magnetic fields, and changing magnetic field can induce electric fields. Together these changing fields can waves of electromagnetism we call light. Light isn’t a separate physical phenomenon, but is due to the fact that electricity and magnetism are connected both physically and mathematically.
Now you might be wondering about gravitational fields. Since the forces of gravity are similar to the forces between charges, doesn’t that imply that there should be a partner to gravity? Some sort of magnetogravity field? It would if gravity was a vector field, but it turns out gravity is a different kind of field altogether.
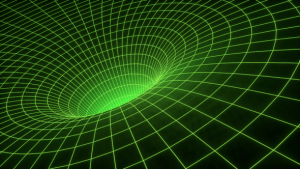
Although the simple representation of vectors is as an arrow, the mathematics is a bit more subtle. Not everything that has a magnitude and direction is a vector. For example, the Sun radiates light outward (direction) at a specific rate (magnitude), but that isn’t a vector. Mathematically, vectors are defined by things like how they add together, and how they transform in different frames of reference. While vectors can be represented by arrows in a physical space, that’s not the only thing they can be. The concept of a vector can also be generalized. You might remember from last time that gravity is actually a geometric property of bendable space and time. For this you need a mathematical quantity that can not only describe changes in quantity and orientation, but also volume and twisting and shear. This is done through a generalization of vectors known as tensors. Gravity isn’t a vector field, but the properties space and time that describe gravity are a tensor field known as the metric tensor. Since vector fields are a special case of tensor fields, gravity can be approximated as a vector field of gravitational force. Tensors are also useful in electromagnetism, since an electromagnetic field can also be described as a single tensor field.
So the arrows of simple forces pointed us to the general concepts of vectors and tensors, and it led us to a deeper understanding of both electromagnetism and gravity.
Next time: Just as geometry and vectors can be generalized into more abstract forms, so can numbers. By generalizing numbers beyond the familiar we’ve been able to understand the imaginary aspects of quantum theory.